Section01_定义与性质
| 域 | 积分号 | 例 |
|---|---|---|
| 线性 | ||
| 面状 |
背景
- 已知密度函数 求钢板的质量
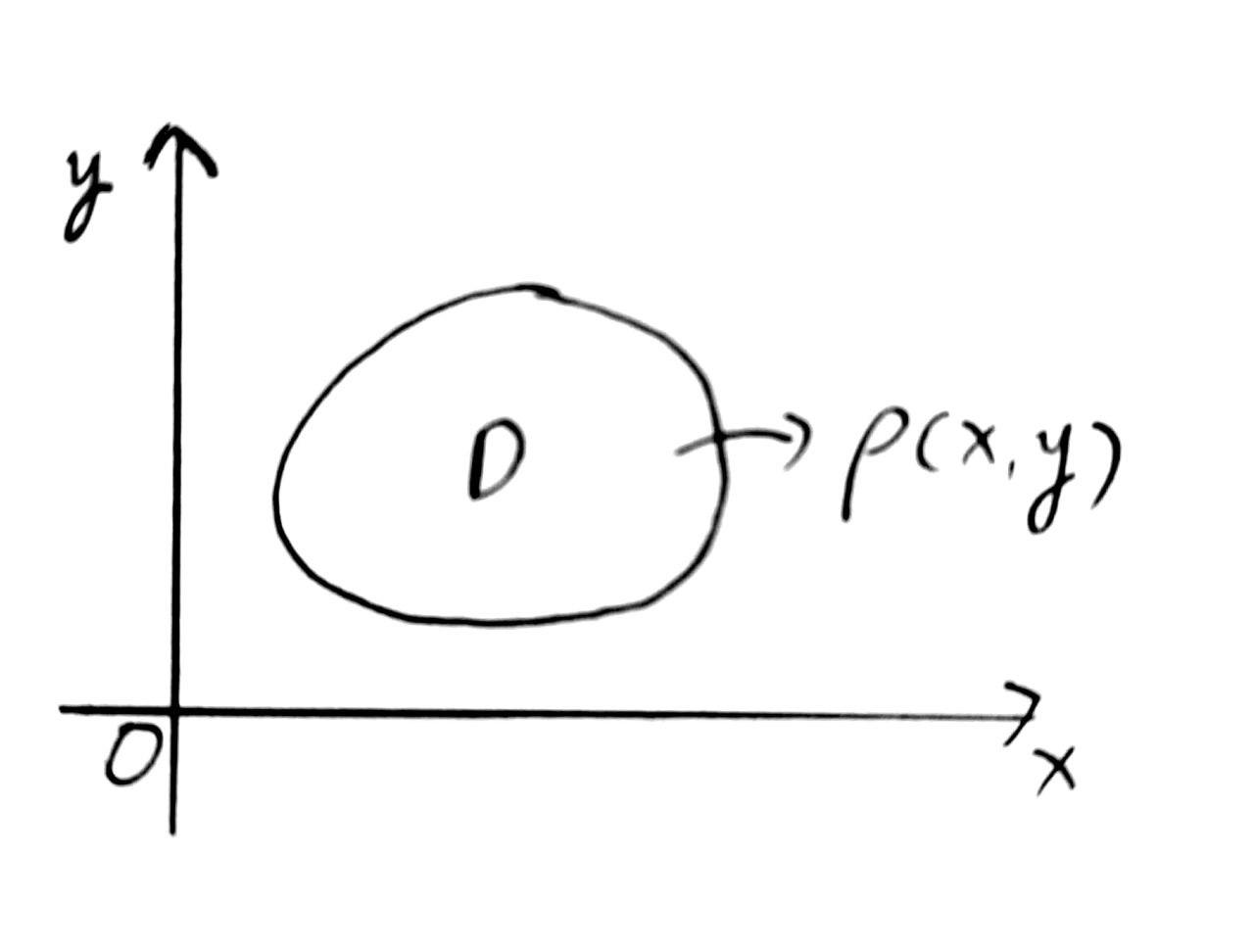
- 将 划分为
- 为 直径的最大者
- 求体积
- 将 划分为
- 为 直径的最大者
定义
- 为 平面上的有界闭区域, 在 上有界
- 将 划分为
- 作
- 为 直径的最大者
- 若 ,则称此极限为 在 上的二重积分,记为 ,即
性质
- 重点 积分中值定理: 为有界闭区间, 在 上连续,则 ,使
- 例 ,求
- 对称性
- 关于左右对称(关于 轴或关于 对称),若右侧为
- 关于 对称
- 例 如下图所示,求

- 例 如下图所示,求