Section03_其他知识点
凹凸性
定义
- 对于 ,若 且 有 称 在 上为凹函数
- 对于 ,若 且 有 称 在 上为凸函数
Notes 若 两侧凹凸性不同, 为拐点
判别法
- Th 设,内二阶可导
- , 在 上为凹函数
- , 在 上为凸函数
例题
- 例1 ,是否为拐点?
渐近线
定义
- 水平渐近线 若 ,称 为水平渐近线。最多仅有两条,且与斜渐近线互斥
- 铅直渐近线 若 满足其一,则为铅直渐近线。铅直渐近线,仅可能存在于间断点处
- 斜渐近线 若, ,称 为斜渐近线
例题
- 例1 ,求渐近线
- 例2
例3
弧微分
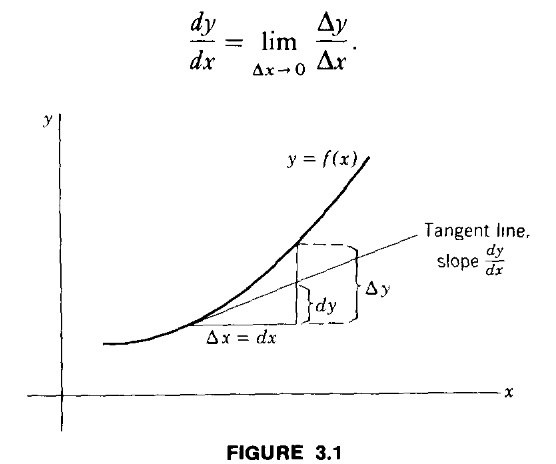
: 即
- : 即