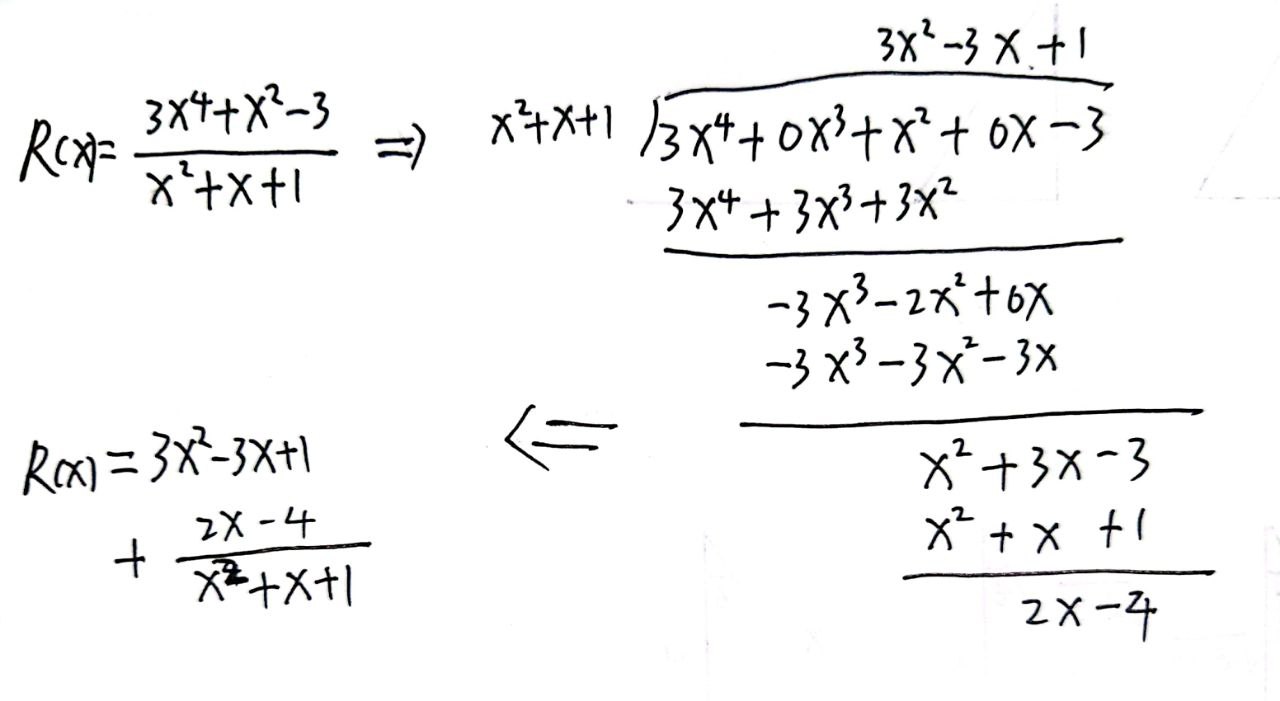Section02_特定函数的不定积分
∫R(x)⋅dx
定义
- R(x)=Q(x)P(x),其中P(x),Q(x)为多项式
- 若 degP<degQ,R(x)为真分式
- 若 degP≥degQ,R(x)为假分式
原则
- 原则一 若R(x)为假分式,R(x)=多项式+真分式,方法如下图所示:
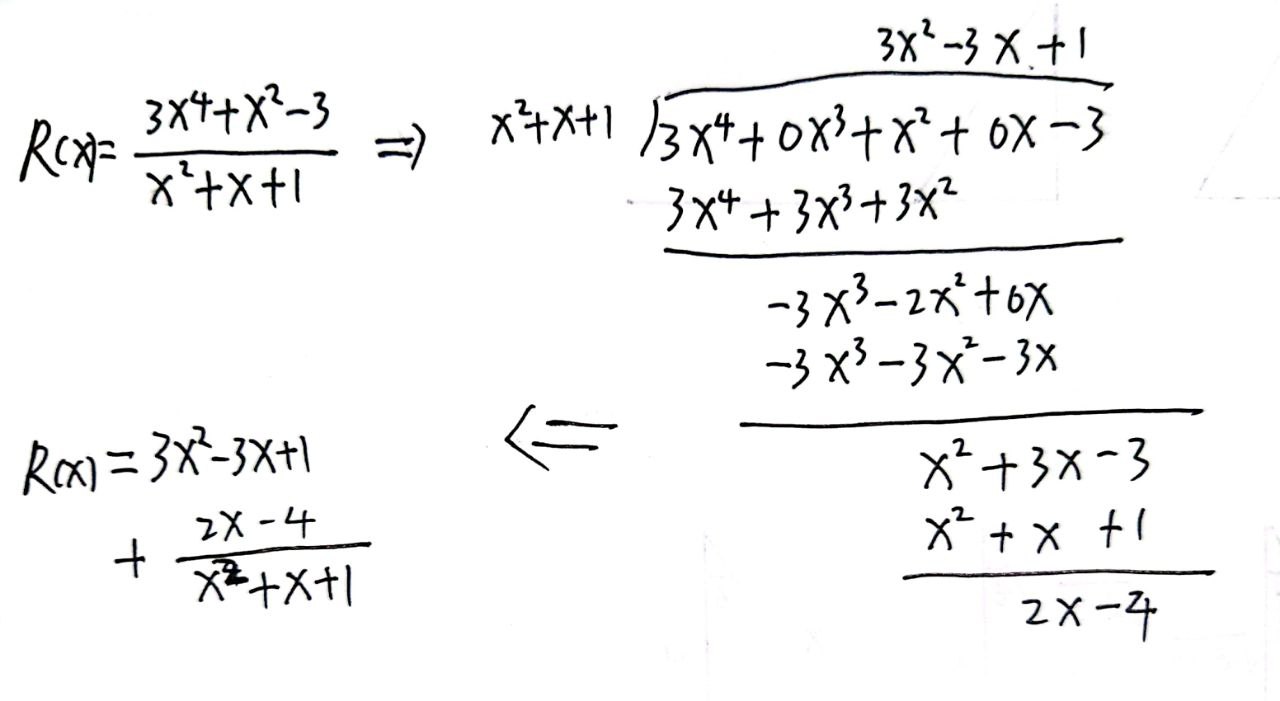
- 原则二 若 R(x) 为真分式{分子不动分母因式分解⇒拆分为部分之和,例
- (2x−1)(x+1)3x−2=2x−1A+x+1B
- (x−2)(x+1)3x3−4x2+1=x−2A+x+1B+(x+1)2C+(x+1)3D
- (2x+1)(x2+1)x2−3x+1=2x+1A+x2+1Bx+C
- x2(x2+x+1)3x2−1=xA+x2B+x2+x+1Cx+D
例题
- 例1 ∫x2−x−121⋅dx
∫x2−x−121⋅dx=∫(x+3)(x−4)1⋅dx=71∫(x−41−x+31)⋅dx=71ln∣∣x+3x−4∣∣+C
- 例2 ∫x2+2x+2dx
∫x2+2x+21⋅dx=∫(x+1)2+11⋅d(x+1)=arctan(x+1)+C
- 例3 x2−x−25x−1⋅dx
∫x2−x−25x−1⋅dx=∫(x−2)(x+1)5x−1⋅dx=∫(x−23+x+12)⋅dx=3ln∣x−2∣+2ln∣x+1∣+C
- 例4 ∫x2+x+1x+2
∫x2+x+1x+2⋅dx=21∫x2+x+1d(x2+x+1)+23∫(x+21)2+(23)21⋅d(x+21)=21ln(x2+x+1)+23⋅32arctan32x+1+C
- 例5 ∫x(1+x2)3x+2⋅dx
∫x(1+x2)3x+2⋅dx=∫(x2+1+x2−2x+3)⋅dx=2ln∣x∣+3arctanx−∫1+x22x⋅dx=2ln∣x∣+3arctanx−ln(1+x2)+C
- 例6 ∫x2(1+x)x3+3⋅dx
∫x2(1+x)x3+3⋅dx=∫x2(1+x)x2(1+x)−x2+3⋅dx=x+∫(x2−3x+3+1+x2)⋅dx=x−3ln∣x∣−3x1+2ln∣1+x∣+C
- 例7 ∫x(x4+3)dx⋅dx
∫x(x4+3)dx⋅dx=∫x4(x4+3)x3⋅dx=41∫x4(x4+3)dx4=121lnx4−121ln(x4+3)
- 例8 ∫x4+1x2+1⋅dx
∫x4+1x2+1⋅dx=∫x2+x211+x21⋅dx=∫(x−x1)2+(2)2d(x−x1)=21arctan2x−x1+C
无理函数的不定积分
Case 1 无需化为有理
- 例1 ∫x(1+x)dx
原式=2∫1+xdx=2arctanx+C
- 例2 ∫x−x2dx⋅dx
原式=2∫1−xdx=2arcsinx+C
- 例3 ∫1−x1+x⋅dx
原式=∫1−x21+x⋅dx=arcsinx−21⋅21−x2+C
Case 2 化为有理
- 例1 ∫ex⋅dx
原式x=t2∫2t×et⋅dt=∫2t⋅det=2tet−∫2et⋅dt=2tet−2et+C=2xex−2ex+C
- 例2 ∫1+xdx
原式x=t2∫1+t2t⋅dt=∫(2−1+t2)⋅dt=2t−2ln∣1+t∣+C=2x−2ln(1+x)+C
三角有理函数的不定积分
- 例1 ∫1+cosxdx⋅dx
原式=