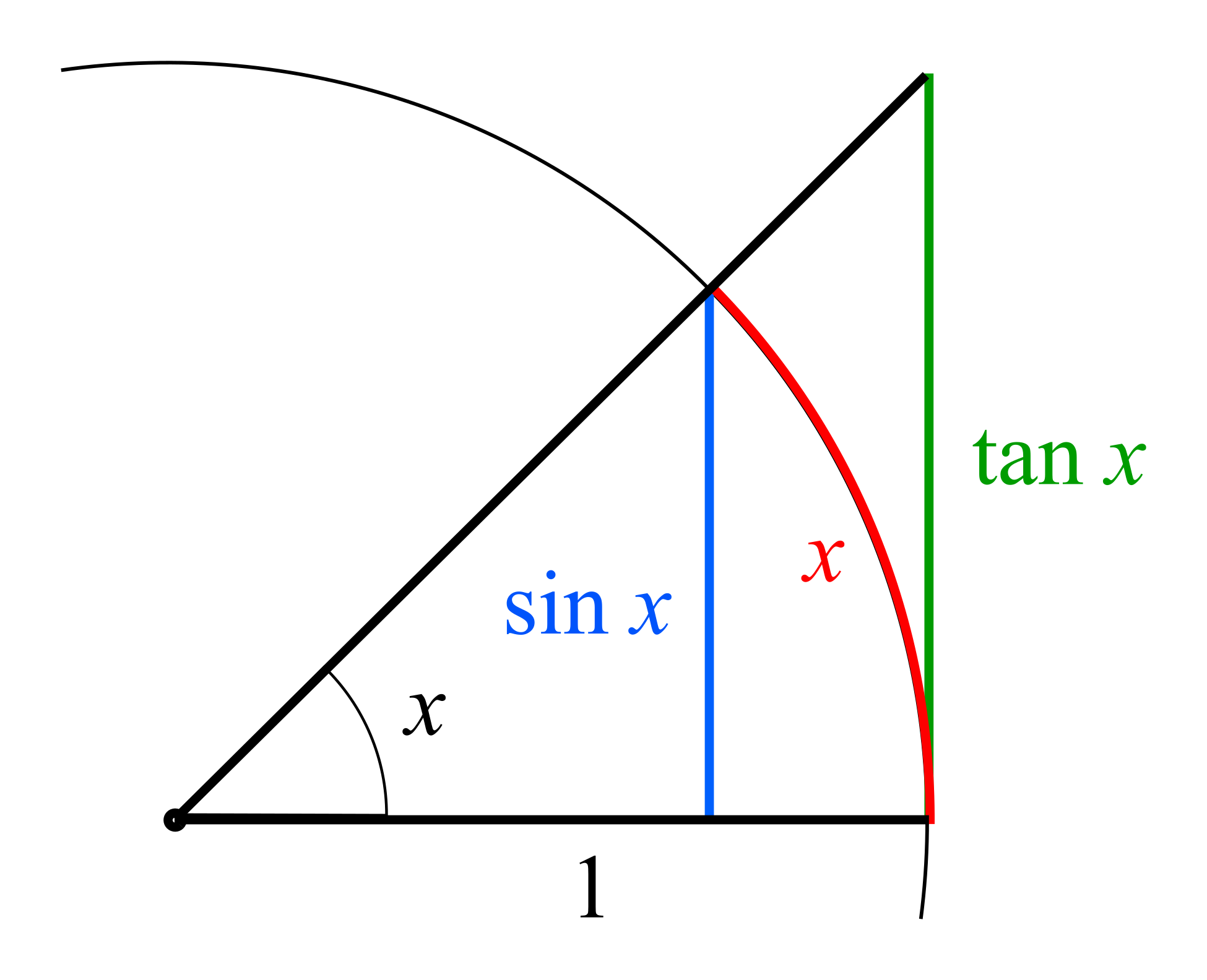Section03_无穷小

定义

1. 若 $\lim_{x\to a} f(x)= 0$，则称 $f(x)$ 为 $x\to a$ 时为无穷小
   1. 层次：设 $\alpha(x) \to 0, \beta(x) \to 0$
      1. $\lim\frac{\beta}{\alpha}=0$ 称 $\beta$ 为 $\alpha$ 的高阶无穷小，记为 $\beta = o(\alpha)$
      2. $\lim \frac{\beta}{\alpha}=k(k\neq 0, \infty)$ 称 $\beta$ 为 $\alpha$ 的同阶无穷小，记为 $\beta = O(\alpha)$
      3. $\lim \frac{\beta}{\alpha} = 1$ 称 $\beta$ 为 $\alpha$ 的等价无穷小，记为 $\alpha\sim\beta$

性质

1. 一般性质
   1. 设 $\alpha\to 0$,$\beta\to 0$，则$\begin{cases}\alpha\pm\beta\to 0\\\alpha\beta\to 0\\ k\alpha \to 0 \end{cases}$
   2. 设 $\vert\alpha\vert\le M,\beta\to 0$，则 $\alpha\beta\to 0$ （单调有界函数同无穷小之积还是无穷小）
   3. $\lim f(x) = A\Leftrightarrow f(x) = A + \alpha\ (\alpha\to 0)$
2. 等价性质
   1. $\begin{cases} \alpha\sim\alpha \\ \alpha\sim\beta\Rightarrow\beta\sim\alpha \\ \alpha\sim\beta,\beta\sim\gamma\Rightarrow\alpha\sim\gamma \end{cases}$
   2. $\alpha\sim\alpha_{1}, \beta\sim\beta_{1} \text{ and } \lim\frac{\beta_{1}}{\alpha_{1}}=A \Rightarrow \lim\frac{\beta_{2}}{\alpha_{2}} = A$
3. 常用等价无穷小 (When $x\to 0$)
   1. $x\sim\sin(x)\sim\tan(x)\sim\arcsin(x)\sim\arctan(x)\sim\ln(1+x)\sim e^{x}-1$
   2. $1-\cos(x)\sim\frac{1}{2}x^{2}$
   3. $(1+x)^{a}-1\sim ax$

重要极限

$\text{If } x\in(0,\frac{\pi}{2})\Rightarrow \sin(x)<x<\tan(x)$

1. $\displaystyle{\lim_{\Delta\to 0}\frac{\sin(x)}{x}=1}$
2. $\displaystyle{\lim_{\Delta\to 0}{(1+\Delta)^{\frac{1}{\Delta}}}=e}$

型三：不定型

常见类型

• 第一梯队 $\frac{0}{0},1^{\infty}$
• 第二梯队 $\frac{\infty}{\infty}, 0\times\infty,\infty-\infty,\infty^{0},0^{0}$

$\frac{0}{0}$型

常见解法

1. 三大习惯
   1. $u(x)^{v(x)}\Rightarrow e^{v(x)\ln u(x)}$
   2. $\ln(\cdots)\Rightarrow\ln(1+\Delta)\sim\Delta\ (\Delta\to 0)$
   3. $(\cdots)-1\Rightarrow\begin{cases}e^{\Delta}-1\sim\Delta\\(1+\Delta)^{a}-1\sim a\Delta\end{cases}\ (\Delta\to 0)$
2. 常识
   1. $x-\ln(1+x)\sim \frac{1}{2}x^2$
   2. $x, \sin(x), \tan(x), \arcsin(x),\arctan(x)$中，任意两者差为三阶无穷小
3. 误区
   1. $\displaystyle{\lim_{x\to 0}\frac{e^{-x^{2}}+\cos(x)-2}{x\sin(x)}} = \lim_{x\to 0}\frac{(e^{-x^{2}}-1)+(\cos(x)-1)}{x^{2}}\color{#D0104C}{=}\frac{-x^{2}-\frac{1}{2}x^{2}}{x^{2}}=-\frac{3}{2}$
   2. $\displaystyle{\lim_{x\to 0}\frac{x-\sin(x)}{x^{3}}}\color{#D0104C}{\neq}\lim_{x\to 0}\frac{x-x}{x^{3}}$

注意：加减用等价无穷小替换时，上下应该为精确度相同；而乘除不管

例题

• 例1 $\displaystyle{\lim_{x\to 0}\frac{(1+2x)^{\sin(x)}-1}{x^{2}}}$
  • 解 $$\begin{split} & \lim_{x\to 0}\frac{(1+2x)^{\sin x}-1}{x^{2}} \\ = & \lim_{x\to 0}\frac{e^{\sin x\ln(1+2x)}-1}{x^{2}}\\ = & \lim_{x\to 0}\frac{\sin x\ln(1+2x)}{x^{2}} \\ = & \lim_{x\to 0}\frac{2x^{2}}{x^{2}} \\ = & 2 \end{split}$$
• 例2 $\displaystyle{\lim_{x\to 0}\frac{\tan x -\sin x}{x^{3}}}$
  • 解 $$\begin{split} & \lim_{x\to 0}\frac{\tan x -\sin x}{x^{3}} \\ = & \lim_{x\to 0}\ \frac{\tan x}{x}\cdot\frac{1-\cos x}{x^{2}}\\ = & \lim_{x\to 0}\ \frac{x}{x}\cdot\frac{\frac{1}{2}x^2}{x^{2}}\\ = & \frac{1}{2} \end{split}$$
• 例3 $\displaystyle{\lim_{x\to 0}\frac{\sqrt{1+\tan x}-\sqrt{1+x}}{x^{3}}}$
  • 解 $$\begin{split} & \lim_{x\to 0}\frac{\sqrt{1+\tan x}-\sqrt{1+x}}{x^{3}} \\ = & \lim_{x\to 0}\frac{1}{\sqrt{1+\tan x} + \sqrt{1+x}}\frac{\tan x -x}{x^{3}}\\ = & \frac{1}{2}\lim_{x\to 0}\frac{\sec^{2} x -1}{3x^{2}}\text{ according to the L'hopital's Rule} \\ = & \frac{1}{6}\lim_{x\to 0}\frac{\tan^{2} x}{x^{2}} \\ = & \frac{1}{6}\lim_{x\to 0}\frac{x^{2}}{x^{2}} =\frac{1}{6}\\ \end{split}$$
• 例4 $\displaystyle{\lim_{x\to 0}\frac{e^{\arcsin x}-e^{x}}{x^{3}}}$
  • 解 $$\begin{split} & \lim_{x\to 0}\frac{e^{\arcsin x}-e^{x}}{x^{3}} \\ = & \lim_{x\to 0}e^{x}\frac{e^{\arcsin x-1}-x}{x^{3}} \\ = & \lim_{x\to 0}\frac{\arcsin x -x}{x^{3}}\text{ according to the L'hopital's Rule} \\ = & \lim_{x\to 0}\frac{\frac{1}{\sqrt{1+x^{2}}}-1}{3x^{2}} \\ = & \frac{1}{3}\lim_{x\to 0}\frac{1/2x^{2}}{x^{2}}=\frac{1}{6}\\ \end{split}$$
• 例5 $\displaystyle{\lim_{x\to 0}\frac{\ln\frac{x}{\sin x}}{x^{2}}}$
  • 解 $$\begin{split} & \lim_{x\to 0}\frac{\ln\frac{x}{\sin x}}{x^{2}} \\ = & \lim_{x\to 0}\frac{\ln(\frac{x - \sin x}{\sin x}+1)}{x^{2}} \\ = & \lim_{x\to 0}\frac{\frac{x-\sin x}{\sin x}}{x^{2}} \\ = & \lim_{x\to 0}\frac{x-\sin x}{x^{3}} \text{ according to the L'hopital's Rule} \\ = & \lim_{x\to 0}\frac{1-\cos x}{3x^{2}} = \lim_{x\to 0}\frac{\frac{1}{2}x^{2}}{3x^{2}} = \frac{1}{6} \end{split}$$
• 例6 $\displaystyle{\lim_{x\to 0}\frac{\big(\frac{1+\cos x}{2}\big)^{x}-1}{x^{3}}}$
  • 解 $$\begin{split} & \lim_{x\to 0}\frac{\big(\frac{1+\cos x}{2}\big)^{x}-1}{x^{3}} \\ = & \lim_{x\to 0}\frac{e^{x\ln(\frac{1+\cos x}{2})}-1}{x^{3}} \\ = & \lim_{x\to 0}\frac{x\ln(\frac{1+\cos x}{2})}{x^{3}} \\ = & \lim_{x\to 0}\frac{\ln(\frac{\cos x-1}{2}+1)}{x^{2}} \\ = & \lim_{x\to 0}\frac{\cos x -1}{2x^{2}} \\ = & \lim_{x\to 0}\frac{-\frac{1}{2}x^{2}}{2x^{2}} = -\frac{1}{4} \\ \end{split}$$
• 例7 $\displaystyle{\lim_{x\to 0}\frac{[\sin x-\sin(\sin x)]\sin x}{x^{4}}}$
  • 解 $$\begin{split} & \lim_{x\to 0}\frac{[\sin x-\sin(\sin x)]\sin x}{x^{4}} \\ = & \lim_{x\to 0}\frac{[\sin x-\sin(\sin x)]\sin x}{\sin^{4}x} \\ = & \lim_{x\to 0}\frac{\sin x-\sin(\sin x)}{\sin^{3}x} \\ & \text{Assume }\sin x \text{ as } t \\ & \text{The original equaltion} = \lim_{t\to 0}\frac{t-\sin t}{t^{3}} \\ = & \lim_{t\to 0}\frac{1-\cos t}{3t^{2}} \\ = & \lim_{t\to 0}\frac{\frac{1}{2}x^{2}}{3t^{2}} = \frac{1}{6} \end{split}$$
• 例8 $\displaystyle{\lim_{x\to 0}\frac{x^2\cos^2 x-\sin^2 x}{x^4}}$
  • 解 $$\begin{split} & \lim_{x\to 0}\frac{x^2\cos^2 x-\sin^2 x}{x^4} \\ = & \lim_{x\to 0}\frac{(x\cos x + \sin x)}{x}\cdot \frac{(x\cos x - \sin x)}{x^{3}} \\ = & \lim_{x\to 0}\frac{(x\cos x + \sin x)}{x}\cdot \frac{(x\cos x - \sin x)}{x^{3}} \\ = & \lim_{x\to 0}(\cos x + \frac{\sin x}{x})\cdot\frac{x\cos x - \sin x}{x^{3}} \\ = & 2\lim_{x\to 0}\frac{\cos x - x\sin x- \cos x}{3x^{2}} \\ = & 2\lim_{x\to 0}\frac{-x\sin x}{3x^{2}} = -\frac{2}{3} \end{split}$$

$1^{\infty}$型

常见解法

1. 凑$(1+\Delta)^{\frac{1}{\Delta}}\ (\Delta \to 0)$
2. 恒等变形

例题

• 例1 $\displaystyle{\lim_{x\to 0}(1-x\sin x)^{\frac{1}{x-\ln(1+x)}}}$
• 解 $$\begin{split} & \lim_{x\to 0}(1-x\sin x)^{\frac{1}{x-\ln(1+x)}} \\ = & \lim_{x\to 0}(1-x\sin x)^{\frac{1}{x-\ln(1+x)}} \\ = & \lim_{x\to 0}\{(1-x\sin x)^{-\frac{1}{x\sin x}}\}^{-\frac{x\sin x}{x-\ln(1+x)}} \\ = & e ^{-\lim_{x\to 0}\frac{x\sin x}{x-\ln(1+x)}} = e^{-2} \end{split}$$
• 例2 $\displaystyle{\lim_{x\to \infty}\bigg(\cos\frac{1}{x}\bigg)^{x^{2}}}$
• 解 $$\begin{split} & \lim_{x\to \infty}\bigg(\cos\frac{1}{x}\bigg)^{x^{2}} \\ = & \lim_{x\to \infty}\bigg\{\bigg[1+(\cos\frac{1}{x}-1)\bigg]^{\frac{1}{\cos\frac{1}{x}-1}}\bigg\}^{x^{2}(\cos\frac{1}{x}-1)} \\ = & e^{\lim_{x\to\infty}\frac{\cos\frac{1}{x}-1}{\frac{1}{x^{2}}}} \\ & \text{let } t = \frac{1}{x} \\ & \text{The Original equation}=e^{\lim_{t\to0}\frac{\cos t-1}{t^{2}}}= e^{-\frac{1}{2}} \end{split}$$
• 例3 $\displaystyle{\lim_{x\to 0}\bigg(\frac{\arcsin x}{x}\bigg)^{\frac{1}{x^{2}}}}$
• 解 $$\begin{split} & \lim_{x\to 0}\bigg(\frac{\arcsin x}{x}\bigg)^{\frac{1}{x^{2}}} \\ = & \lim_{x\to 0}\bigg\{\bigg[1+\frac{\arcsin x - x}{x}\bigg]^{\frac{x}{\arcsin x - x}}\bigg\}^{\frac{\arcsin x - x}{x^{3}}} \\ = & e ^{\lim_{x\to 0}\frac{\arcsin x - x}{x^{3}}} = e^{\lim_{x\to 0}\frac{(1-x^{2})^{-\frac{1}{2}-1}}{3x^{2}}} \\ = & e^{\lim_{x\to 0}\frac{\frac{1}{2}x^{2}}{3x^{2}}} = e^{\frac{1}{6}} \end{split}$$
• 例4 $\displaystyle{\lim_{x\to 0}\bigg(\frac{1+\tan x}{1+\sin x}\bigg)^{\frac{1}{x^{3}}}}$
• 解 $$\begin{split} & \lim_{x\to 0}\bigg(\frac{1+\tan x}{1+\sin x}\bigg)^{\frac{1}{x^{3}}} \\ = & \lim_{x\to 0}\bigg\{\bigg(1 + \frac{\tan x -\sin x}{1+\sin x}\bigg)^{\frac{1+\sin x}{\tan x- \sin x}}\bigg\}^{\frac{\tan x - \sin x}{x^{3}(1+\sin x)}} \\ = & e^{\lim_{x\to 0}\frac{1}{1+\sin x}\cdot \frac{\tan x-\sin x}{x^{3}}} \\ = & e^{\lim_{x\to 0}\frac{\tan x(1-\cos x)}{x^{3}}} = e^{\frac{1}{2}}\\ \end{split}$$

$\frac{\infty}{\infty}$型

常见解法

1. 洛必达法则
   1. $\displaystyle{\lim_{n\to +\infty} \frac{\ln^{a}x}{x^{b}}=0\quad (a>0,b>0)}$
   2. $\displaystyle{\lim_{n\to +\infty} \frac{x^{a}}{b^{x}}=0\quad (a>0,b>1)}$
2. $\displaystyle{\lim_{n\to +\infty} \frac{a_{m}x^{m}+\cdots}{b_{n}x^{n}+\cdots}=\begin{cases}0&m<n,\\\infty&m>n,\\\frac{a_{m}}{b_{n}}&m=n.\end{cases}}$

例题

• 例1 $\displaystyle{\lim_{x\to \infty}\frac{x^{8}+3x+1}{(x+1)^{a}-(x-1)^{a}}=b,\quad b\ne 0\ne\infty}$，求$a,b$
• 解 $$\begin{array}{ll} \because & (x+1)^{a} = {a\choose 0}x^{a} + {a\choose 1}x^{a-1} +\cdots \\ & (x-1)^{a}={a\choose 0}x^{a}-{a\choose 1}x^{a-1}+\cdots\\ \therefore & (x+1)^{a}-(x-1)^{a} = 2ax^{a-1}+\cdots \\ \therefore & \begin{cases} a-1 = 8 \\ \frac{1}{2a} = b\\ \end{cases}\\ \therefore & \begin{cases} a=9 \\ b=\frac{1}{18} \end{cases}\\ \end{array}$$
• 例2 $\displaystyle{\lim_{x\to \infty}\bigg(\frac{2x^{2}+3x+4}{x-1}-ax-b\bigg)=0}$，求$a,b$
• 解 $$\begin{array}{ll} \because & \frac{2x^{2}+3x+4}{x-1}-ax-b = \frac{(2-a)x^{2}+(3+a-b)x+4+b}{x-1} \\ \therefore & \begin{cases} 2-a=0 \\ 3+a-b=0 \\ \end{cases} \\ \therefore & \begin{cases} a=2 \\ b=5 \end{cases} \\ \end{array}$$
• 例3 $\displaystyle{\lim_{x\to \infty}\frac{\ln(3x^{2}+x+4)}{\ln(2x^{4}-x^{2}+3)}}$
• 解 $$\begin{split} & \lim_{x\to \infty}\frac{\ln(3x^{2}+x+4)}{\ln(2x^{4}-x^{2}+3)} \\ = & \lim_{x\to \infty}\frac{\frac{6x+1}{3x^{2}+x+4}}{\frac{8x^{3}-2x}{2x^{4}-x^{2}+3}} \\ = & \lim_{x\to \infty} \frac{12x^{5}+\cdots}{24x^{5}+\cdots} = \frac{1}{2} \end{split}$$

$\infty-\infty$型

常用解法

1. 有分母 => 通分
2. 无分母 => 尽量变为分母形式

例题

• 例1 $\displaystyle{\lim_{x\to \infty}[x-x^{2}\ln(1+\frac{1}{x})]}$
• 解 $$\begin{split} & \lim_{x\to \infty}[x-x^{2}\ln(1+\frac{1}{x})] \\ = & \lim_{x\to \infty}x^{2}[\frac{1}{x}-\ln(1+\frac{1}{x^{2}})] \\ = & \lim_{x\to \infty}\frac{\frac{1}{x}-\ln(1+\frac{1}{x^{2}})}{\frac{1}{x^{2}}} \\ & \text{let }t = \frac{1}{x}\\ & \text{The original euqation} = \lim_{t\to 0}\frac{t-\ln{(1+t)}}{t^{2}} \\ = & \lim_{t\to 0}\frac{\frac{1}{2}t^{2}}{t^{2}} = \frac{1}{2} \end{split}$$
• 例2 $\displaystyle{\lim_{x\to\infty}[(x+1)\arctan x-\frac{\pi}{2}x]}$
• 解 $$\begin{split} & \lim_{x\to\infty}[(x+1)\arctan x-\frac{\pi}{2}x] \\ = & \lim_{x\to\infty}[x(\arctan x-\frac{\pi}{2})] +\lim_{x\to\infty}\arctan x \\ = & \lim_{x\to\infty}[x(\arctan x-\frac{\pi}{2})] + \frac{\pi}{2}\\ = & \lim_{x\to\infty}\frac{\arctan x-\frac{\pi}{2}}{\frac{1}{x}} +\frac{\pi}{2} \\ = & \lim_{x\to\infty}\frac{\frac{1}{1+x^{2}}}{-\frac{1}{x^{2}}} +\frac{\pi}{2} \\ = & \frac{\pi}{2}-1 \end{split}$$
• 例3 $\displaystyle{\lim_{x\to\infty}(\sqrt{x^{2}+2x+3\sin x}-x)}$
• 解 $$\begin{split} & \lim_{x\to\infty}(\sqrt{x^{2}+2x+3\sin x}-x) \\ = & \lim_{x\to\infty}\frac{2x+3\sin x}{\sqrt{x^{2}+2x+3\sin x}+x} \\ = & \lim_{x\to\infty}\frac{2+3\frac{\sin x}{x}}{\sqrt{1+2\frac{1}{x}+\frac{3\sin x}{x^{3}}}+1} = 1\\ \end{split}$$
• 例4 $\displaystyle{\lim_{x\to 0}\bigg(\frac{1}{x^{2}}- \frac{1}{\arctan^{2} x}\bigg)}$
• 解 $$\begin{split} & \lim_{x\to 0}\bigg(\frac{1}{x^{2}}- \frac{1}{\arctan^{2} x}\bigg) \\ = & \lim_{x\to 0}\frac{\arctan^{2} x-x^{2}}{x^{2}\arctan^{2}x} \\ = & \lim_{x\to 0}\frac{\arctan x+x}{x}\cdot\frac{\arctan x-x}{x^{3}} \\ = & 2\lim_{x\to 0}\frac{\frac{1}{1+x^{2}}-1}{3x^{2}} \\ = & -\frac{2}{3} \end{split}$$

$\infty^{0} \text { and }0^{\infty}$型

常见解法

• 转化为$e^{ln(\cdots)}$形式

例题

• 例1 $\displaystyle{\lim_{x\to 0^{+}}x^{\sin 2x}}$
  • 解 $$\begin{split} & \lim_{x\to 0^{+}}x^{\sin 2x} \\ = & \lim_{x\to 0^{+}}e^{\sin 2x\cdot\ln(x)} \\ = & e^{\lim_{x\to 0^{+}}\sin 2x\cdot\ln(x)} \\ = & e^{\lim_{x\to 0^{+}}2x\cdot\ln(x)} \\ = & e^{2\lim_{x\to 0^{+}}\frac{\ln(x)}{\frac{1}{x}}} \\ = & e^{2 \lim_{x\to 0^{+}}\frac{1/x}{-1/x^{2}}} \\ = & 1 \end{split}$$

$0\times\infty$型

• 转化为$\frac{\infty}{\infty}$或$\frac{0}{0}$型