下图为y=x−1的图像,P为y=f(x)上过原点的切线
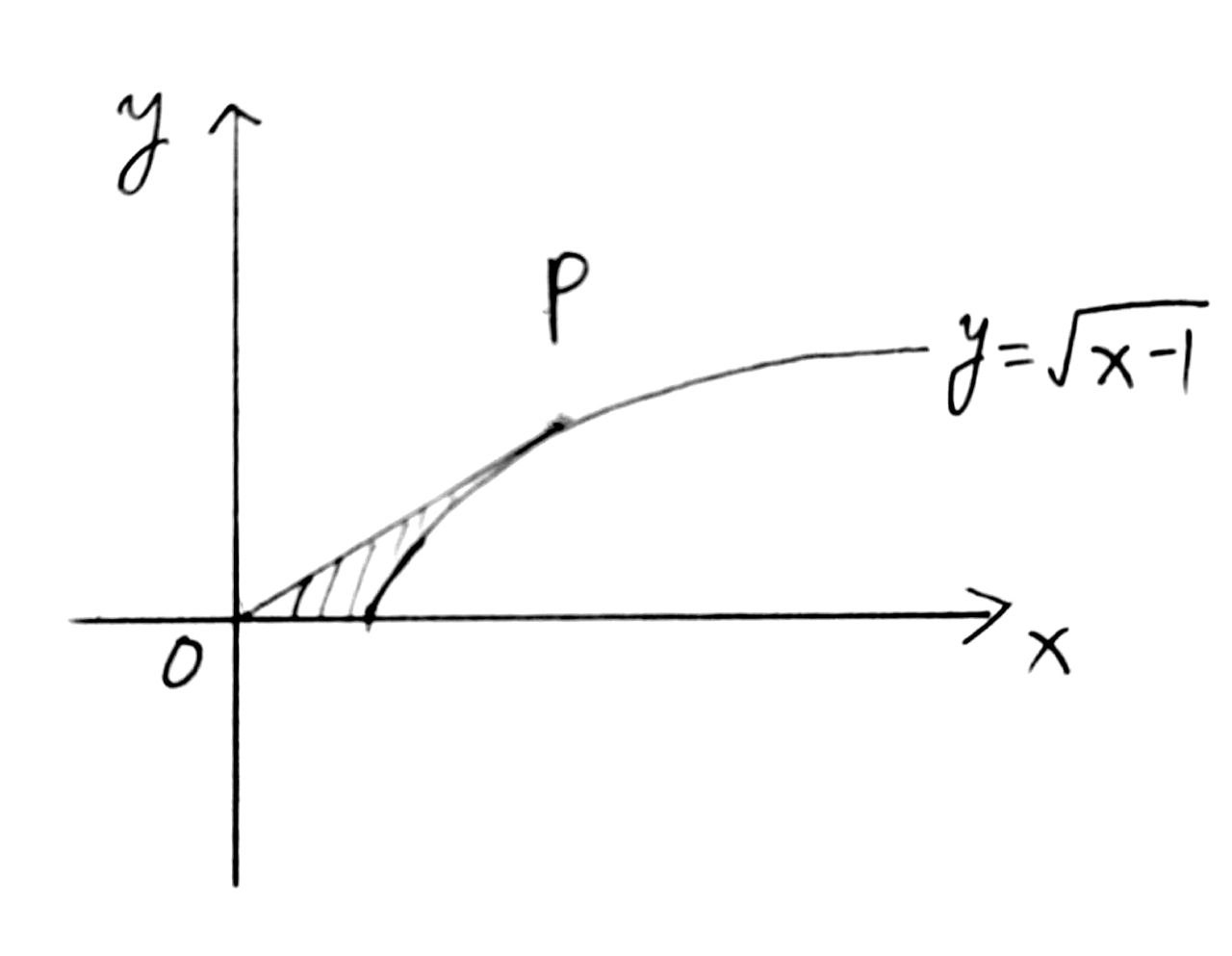
- 求切线方程
∴∵∴∴设P点坐标为(a,a−1)P点切线斜率为y′∣x=a=2a−11方程为y−a−1=2a−11(x−a)切线过原点−a−1=−2a−1a解得a=2切线方程为y=21x
- 求阴影部分面积
A=∫0221x⋅dx−∫12x−1⋅dx=41x2∣∣02−32(x−1)23∣∣12=1−32=31
- 求阴影部分绕x轴一周图形的表面积
∵∴∵∴∴A总=A内+A外A內=2π∫12x−11+[(x−1)′]2⋅dxA内=2π∫12214x−3⋅dx=π⋅41∫124x−3⋅d(4x−3)=4π×32(4x−3)23∣∣12=655−1πA外=2π∫0221x1+[(21x)′]2⋅dxA外=25π∫02x⋅dx=45πx2∣∣02=5πA总=6115−1π
如下图所示,已知阴影为半个椭圆,求其绕x=2旋转一周后的图形的体积
 ∵∴∴取[x,x+dx]∈[−2,2]dV=2(2−x)πydx4x2+y2=1y=1−4x2dV=2π(2−x)1−4x2⋅dxV=2π∫−22(2−x)1−4x2⋅dx=2π∫02[(2−x)1−4x2+(2+x)1−4x2]⋅dx=8π∫021−4x2⋅dxx=2sint8π∫02πcost(2cost)⋅dt=16πI2=4π2
∵∴∴取[x,x+dx]∈[−2,2]dV=2(2−x)πydx4x2+y2=1y=1−4x2dV=2π(2−x)1−4x2⋅dxV=2π∫−22(2−x)1−4x2⋅dx=2π∫02[(2−x)1−4x2+(2+x)1−4x2]⋅dx=8π∫021−4x2⋅dxx=2sint8π∫02πcost(2cost)⋅dt=16πI2=4π2
如下图所示,求该图形绕y轴旋转一周后图形的体积
 ∵∴取[y,y+dy]∈[−1,21]dV=πx2dyx2+y2=1dV=π(1−y2)dyV=π∫−121(1−y2)⋅dy=π(y−31y3)∣−121=89π
∵∴取[y,y+dy]∈[−1,21]dV=πx2dyx2+y2=1dV=π(1−y2)dyV=π∫−121(1−y2)⋅dy=π(y−31y3)∣−121=89π









