Section01_定义与方法
- 原函数 - 若 ,称 为 的原函数
Notes
- 若 有原函数 存在无限个原函数
- 任何两个原函数之差为常数
- 若 连续 存在原函数
- 不定积分 - 设 为 的一个原函数, 为所有原函数,成为不定积分,记为
不定积分工具
基本公式
- 三角函数
- 反三角函数
积分法
换元积分法
第一类换元积分法
原理
- 例1
- 例2
- 例3
- 例4
例5
第二类换元积分法
原理
- 无理化有理化
- 平方和平方差三角代换
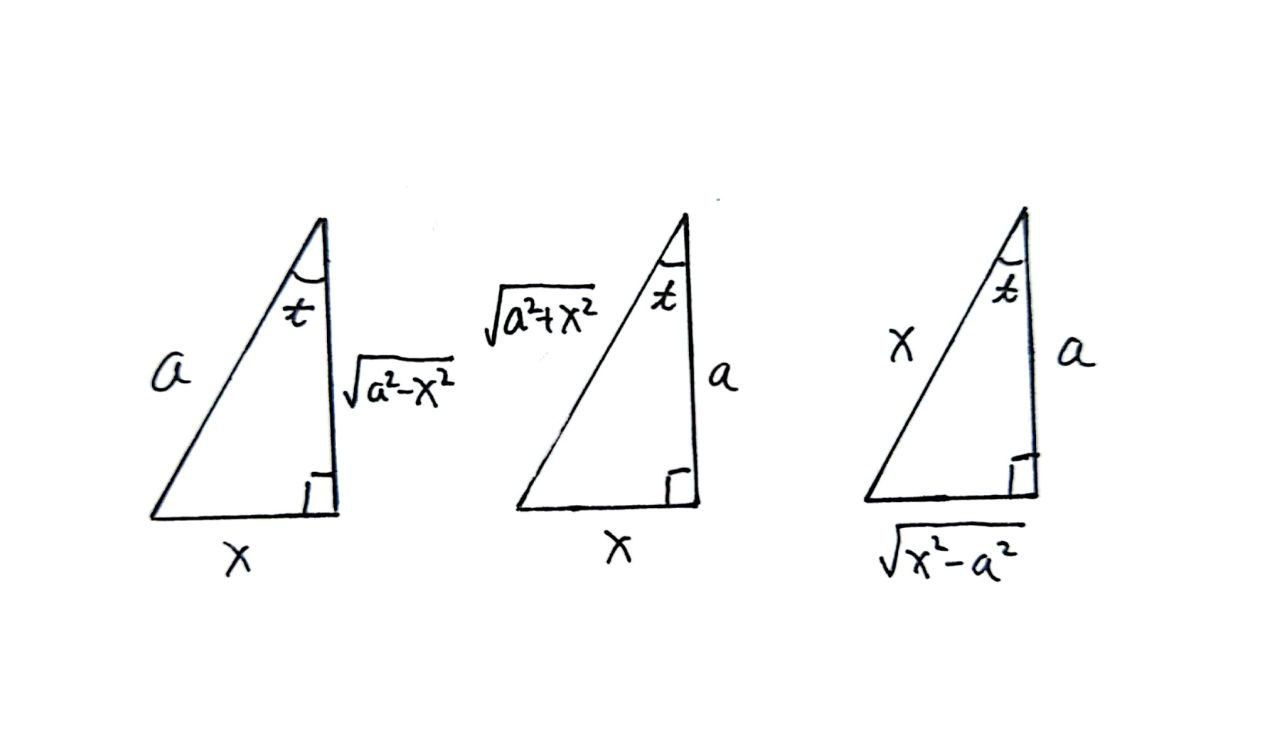
例1
- 例2
- 例3
分部积分
基本思想
- 例
- 例
- 例1
- 例2
- 例3
- 例1
- 例2
- 例
- 例